return to the Geometric Dissections menu

Polygonal dissections

The theory of polygonal dissections and its results are dependent on accepting the Archimedes’ axiom [1]:

(A) For any given two segments, there is a multiple of one of them that exceeds the other.

This assumption is implicit in most presentations of the topic. It can be shown that:

a) Any triangle can be dissected into a parallelogram.

b) Any parallelogram can be dissected into a rectangle.

c) Any rectangle can be dissected into another rectangle of a given side.

Using these preliminary results it can also be proved that:

d) Two plane polygons have the same area if and only if they are equivalent by dissection.

e) The union of two squares is equivalent by dissection to another square.

f) Any rectilinear figure can be dissected into a square.

A graphic illustration of the last result is pictured below, using the terminology in Henderson and Taimina:

Explorers of polygonal equivalence by dissection have found a wealth of constructions that prove the equivalence prima facie.

Here is the dissection of a pentagon into a heptagon:

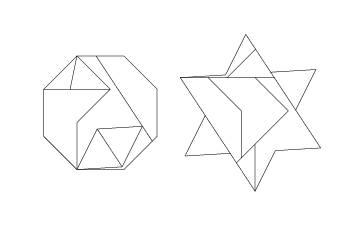
and that of an octagon into a hexagonal star :[2]

Below is a wide variety of dissections between pairs of regular polygons:

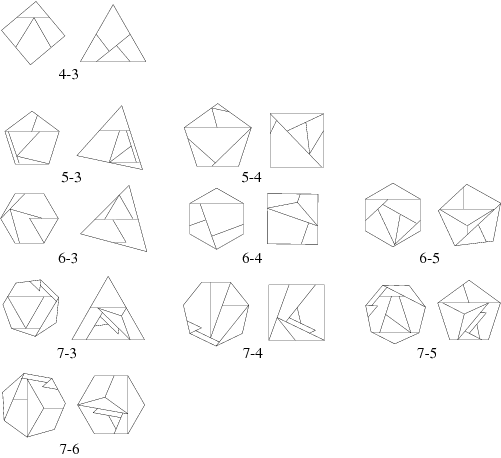
The next group contains more complex dissections:

And here is yet another group, containing regularly-shaped polygonal stars: [3]

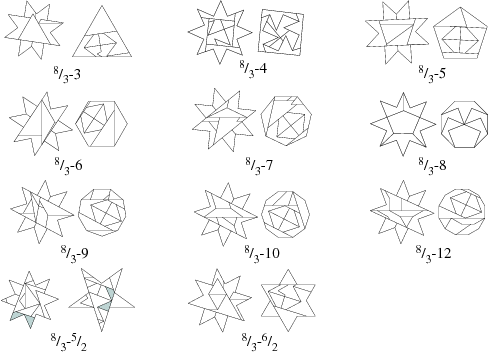
Most of the dissections pictured above can be obtained using variations of the strip methods described in the Recent flourishing sub-module.

Some dissections are not unique. Let’s exemplify with several remarkable examples.

Here is a dissection of a regular hendecagon (11-sides) to a square [4]

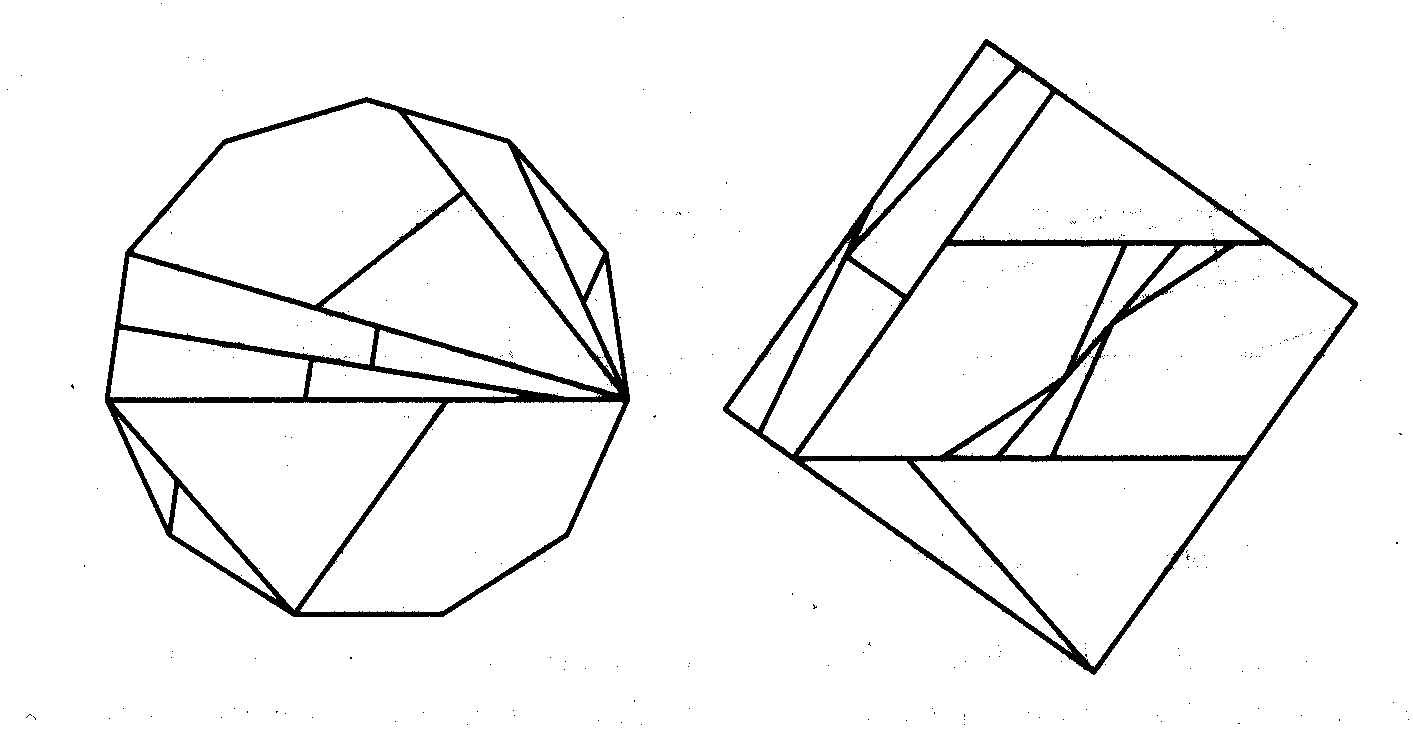
and a different one, also of a hendecagon to a square,

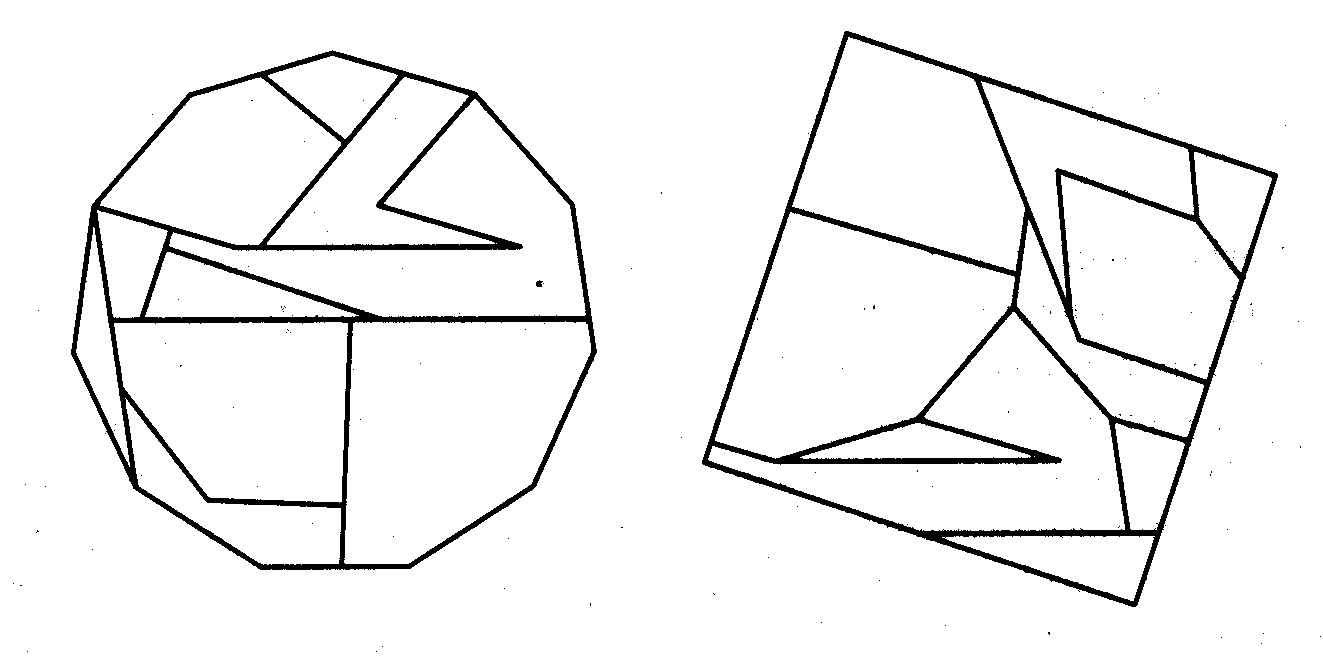
The latter dissection can be found either by using the following cross-positioning of two strips

or by this one:

Similarly, for the dissection of a 15-gon to a square

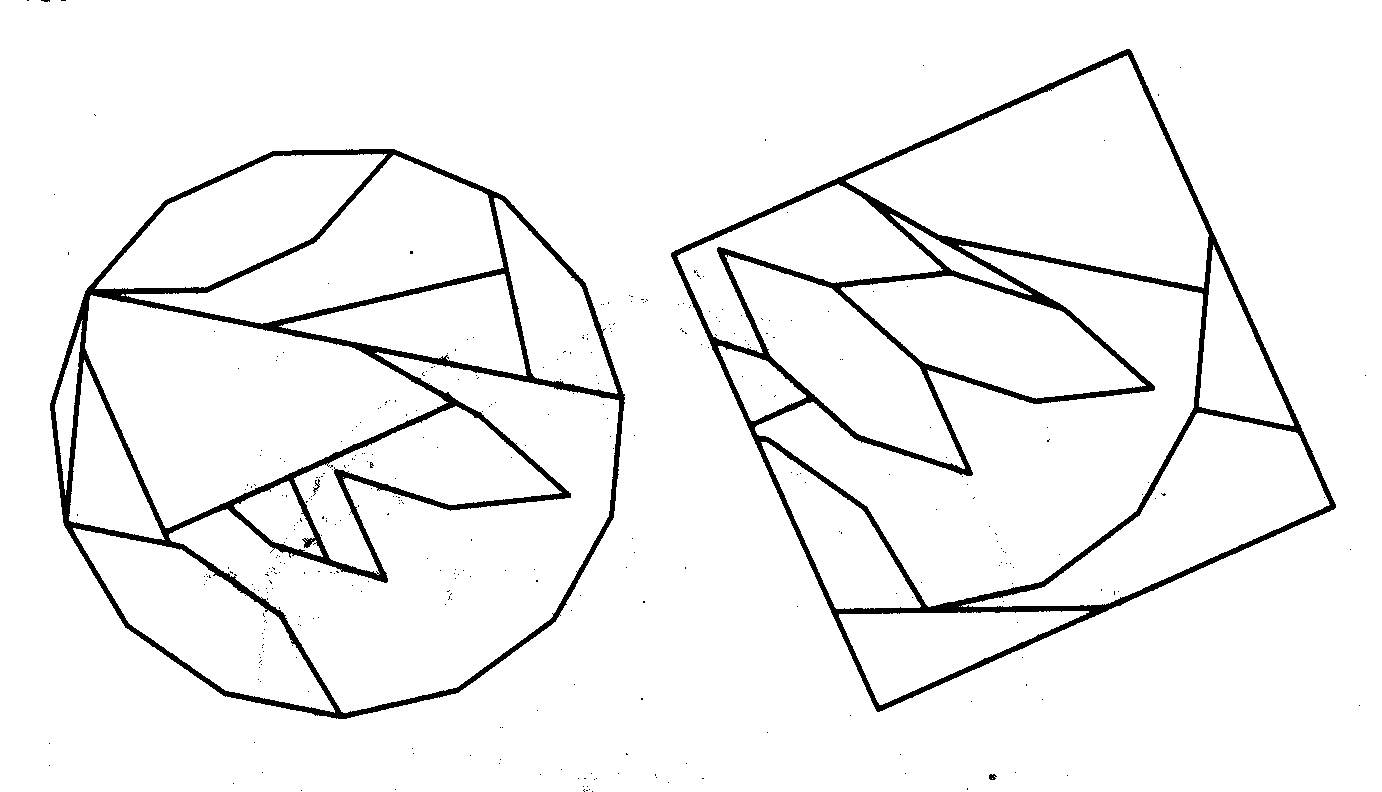
either the following cross-position of strips can be used

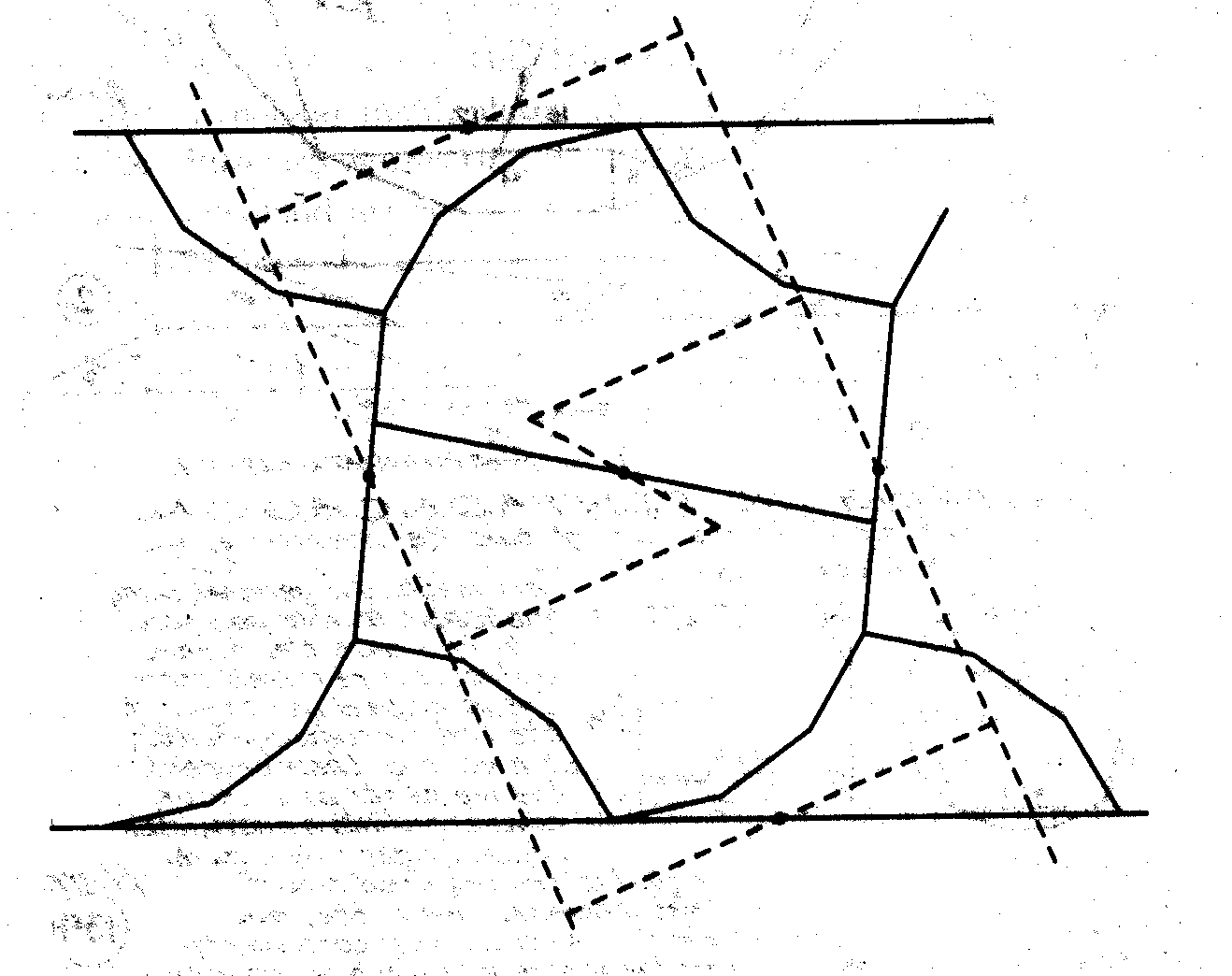
or this one

ENDNOTES: